NASA Visiting Student Enrichment Program: 2003 Shupe Report

Project Objective:
The objective of this project was to develop a parallel simulation code from a similar single processor code and then run the parallel simulation code on a Beowulf cluster machine. The code I studied utilizes a lattice random path model using entwined paths [2,3] that can be shown to model the quantum mechanical properties of a particle in a box.

Significance:
By running the code on Medusa [4], and confirming our results from simulations on a single processor, we have shown that this parallel environment is an effective tool for computations which simulate simple quantum mechanical systems.

In addition to demonstrating the effectiveness of the parallel environment, a model of this kind may lead to further insights into quantum mechanics, thereby allowing more effective application of our understanding of quantum mechanics. Specifically, a better understanding of the processes underlying the equations of quantum mechanics may facilitate the design and implementation of quantum computation.

Approach:
The basis of our approach was to initially develop the simulation code in a single processor environment, which allowed for easier coding and initial testing. Once we were satisfied with the single processor code, we then ported it to a parallel environment in order to produce better statistics and to more vigorously test the validity of our model.

The first step was to show that the simulation code worked correctly on a single processor machine. The criteria of this validation were that (1) the code successfully stored the projection of each particle's space-time history and when necessary, referenced this history to produce a state change, and (2) that if given initial conditions for the energy eigenfunctions, the eigenfunctions of the particle were shown to persist. The first condition was necessary to improve the convergence of the simulation. At each point in the space-time grid the particle checks the quantum eigenspace and if possible minimizes any fluctuations. If the particle cannot minimize the fluctuations in the eigenspace, it proceeds randomly, determining state changes by a probabilistic procedure. Thus, this model of quantum mechanics is not based solely on a stochastic process (a process governed by probabilities, like the flipping of a coin), since the decision of whether to change stare is not always the result of a probabilistic procedure. The second criterion listed above tested whether or not our method for restricting the entwined walks of the particle to the grid of the box preserved the time evolution of the particle, also known as the Dirac propagator [5]. This criterion tested whereto or not our model embodied in the simulation code produced as a natural result the mechanics of propagation.

Once verified to work correctly on a single processor machine, the simulation code was ported to Medusa. This step was vital to the success of the project, since the basis of the model is a stochastic process of random walks of the particle. Having the ability to simulate more entwined paths,or more particles, through the use of a parallel machine is crucial to improving the statistics of the simulation so as to more readily test the quality of the simulation using the criteria utilized in the single processing environment.

Instead of rewriting the code for the Beowulf parallel environment, the code is kept in its single processor form and an additional program is implemented to delegate tasks between the processors and monitor which processors have completed their tasks and which have not. Each processor simulates the entwined path of one particle in a box, and writes to a file on the processor node the information necessary to generate the particle's entwined path. Using a single computer, the separate files written by all of the processors are compiled into a single file, and then the results are plotted using a visualization utility.

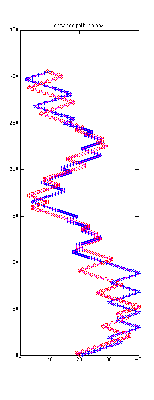
FIG. 1: Entwined path in a box. In this model, entwined paths are confined to a two-dimensional discrete space. In the figure, the y-axis is the time dimension, and the x-axis is the spatial dimension. The axes are scaled by the speed of light, such that objects traveling at the speed of light will move on diagonal paths, similar to the moves of a bishop on a chessboard. In the figure, the blue line can be thought of as representing the path of an electron (moving forward in time) and the red line of a positron (moving backward in time). The box has a width of L, and a height of t return, the return time of one cycle. The entwined path shown represents only one cycle of the code, despite its length and numerous crossings of the red and blue components of the path. Since the return time of this entwined path is quite large, the red and the blue paths have more opportunities to cross (i.e., the electron and the positron have more opportunities to interfere with each other). Once the entwined path has reached the return time, the space-time position is reset to the origin, and another entwined path is generated. This process of entwined path generation is repeated for the predefined number of cycles. Though the code does indeed generate many entwined paths, the entwined paths are in reality a single path since each entwined path begins and ends at a common point in the space-time grid; the point defined by the program to be the origin.

If time permits, the process of converting a single processor code to a parallel environment will be implemented for a measurement scheme. Such a scheme would entail choosing a point on the space-time lattice (x₀, t₀) from which particles can be observed, and then utilizing observation criteria to determine what conditions must be present in order to observe a particle. A particle observed at (x₀, t₀) would be prevented from returning to a time less than t₀, so the particle's path for t < t₀ would remain impaired (a Bohm) path. This process would be repeated for all x (within the boundaries of the box) at t₀, which will produce a distribution of Bohm paths for t = t₀. The characteristics of the distribution will depend on the observation criteria. Assuming that we choose right criteria, the distribution should agree with the Born postulate [6]. If the postulate holds for the measurements taken in the parallel environment, it will be shown that measurement as well as propagation in quantum mechanics are governed by an underlying stochastic process.

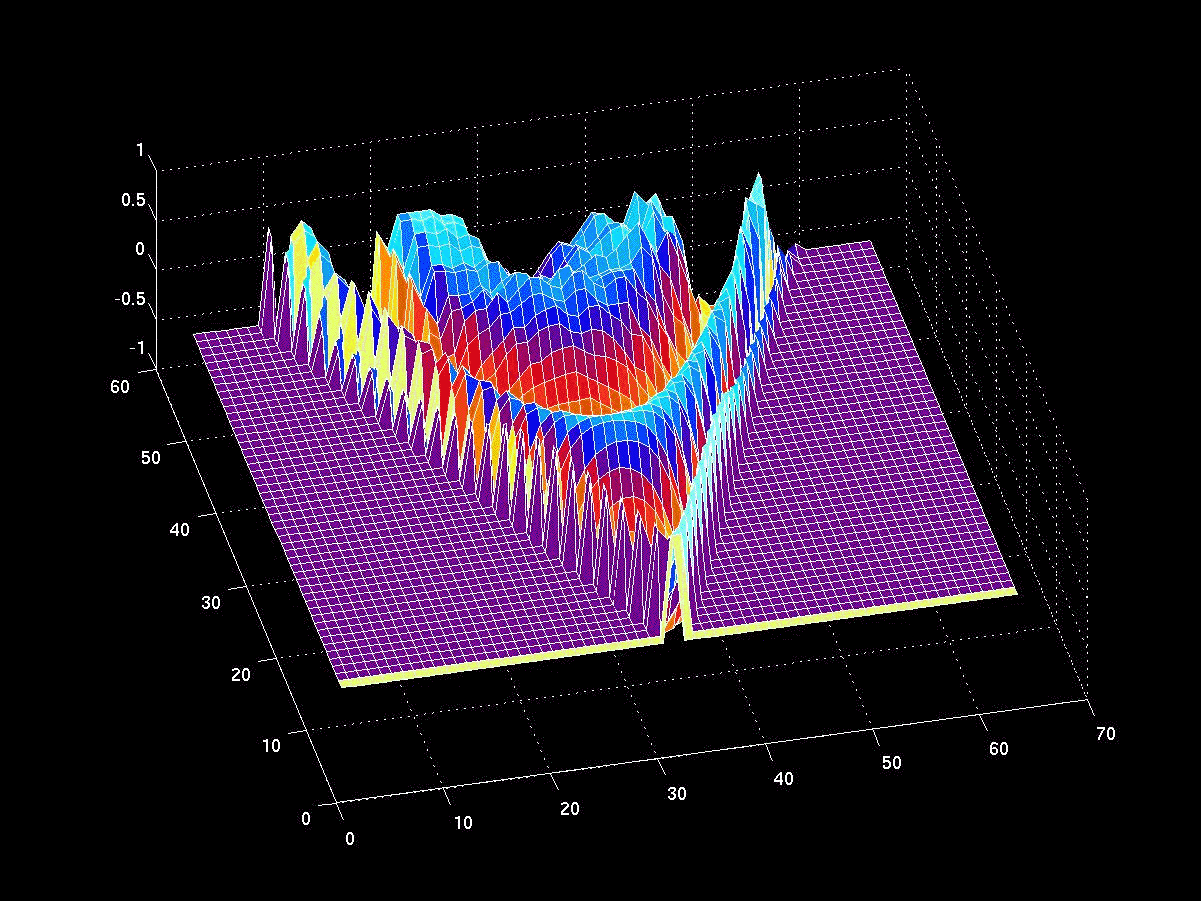
FIG. 2: Dirac propagator for a free particle. The axis running left to right parallel to the page is space, and the axis going into the page is space. This result came from a simulation code which did not retain the space-time history, and was run on Medusa, a Beowulf cluster.

My Contribution:
The algorithm that generates an entwined path in a box [1] was originally written in MATLAB (MathWorks, version 6.5), which was designed for mathematical programming and as such is well suited for our project. If the MATLAB code were to be run on Medusa, however, a copy of MATLAB would have to be installed on each node. This installation process would not only be costly in that it would occupy valuable memory which could otherwise be devoted to running the program, but it would also be quite expensive since each individual copy of MATLAB requires a separate license. As a result, I worked with Dr. Gualtieri to rewrite the MATLAB code in C with the goal of making the code more efficient and cost effective.

This rewriting process was quire arduous and ultimately required much more time than we had expected. As a result, once I completed the rewrite of the first version of the code in C, I investigated the MATLAB C compiler as an alternative to manual coding of later versions of the entwined path algorithm. The program became somewhat unreadable after the conversion process, but did achieve the same results. Therefore, in an effort to accelerate the progress of the project, we elected to use the MATLAB C compiler instead of converting the code manually for later versions of the algorithm.

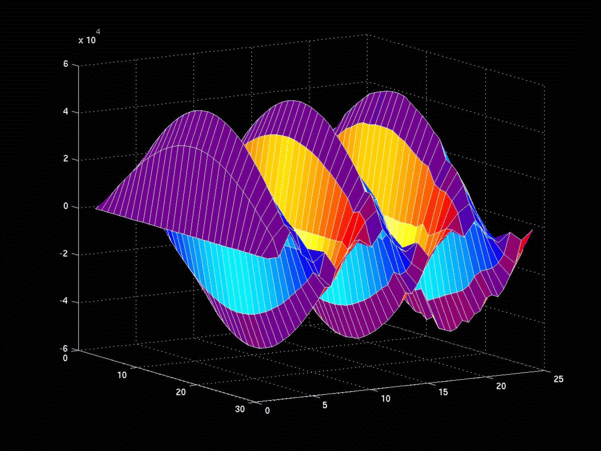
FIG. 3: Time evolution of the ground state for a particle in a box. The axis running left to right parallel to the page is time, and the axis going into the page is space. Notice that the wave-function is jagged at the boundaries of the box, and becomes worse as time progresses. Initially, these rough edges at the boundaries were thought to be a problem with the code, but recently we have found that the problem arises from a property common to all discrete models of the Dirac equation for a particle in the box. That is, given an initial trigonometric condition for the wave-function, the Dirac equation is not separable. This result came from a simulation code which did not retain the space-time history, and was run on a single processor machine.

The simulation code for a free particle has already been run on Medusa, which generated the Dirac propagator for a free particle (Fig. 2). Using the techniques developed in running the free particle code on a parallel machine, I am attempting to run on Medusa the newest version of the simulation code for a particle in a box. If this run is successful, it will be possible to compare the results from a single processor (Fig. 3) to the results from a multiprocessor parallel environment. Despite the increased statistics of the Beowulf cluster simulation, the jagged edges of the wavefunction near the boundaries of the box are expected to linger because they are not related to the stochastic process of the code. Rather, these fluctuations result from the inability of the Dirac equation to separate given trigonometric initial conditions. Future versions of the code will eliminate this problem by incorporating periodic boundary conditions for the box, which allow the Dirac equation to separate given trigonometric initial conditions.

Notes:
[1] G. N. Ord. box-path-generate.m, 2003.
[2] G. N. Ord and J. A. Gualtieri. The feynman propagator from a single path. Physical Review Letters, 89(25):1-4, 2002.
[3] G. N. Ord and R. B. Mann. Entwined paths, difference equations and dirac equation. Preprint, 2002.
[4] A 64 node Beowulf cluster machine. The nodes have 2 processors (AMD Athlon 1.2 Ghz, 512K of cache) each and are connected through a MYRINET (Myricom) network.
[5] The Dirac wave equation includes spin,and is the relativistic generalization of the Schrodinger wave equation. The Dirac propagator is the mathematical device (matrix given by the Dirac equation) by which we move or propagate the wave-function forward through time.
[6] The postulate states that the probability of measurement of a particle in a certain state is the square of the modulus of the wave-function.

Apply To VSEP | VSEP Overview | Previous Years | Home
Visiting Student Enrichment Program (VSEP) Chairperson:
Dr. Marilyn Mack
NASA GSFC/Mail Code 933
Greenbelt, MD 20771
Marilyn.J.Mack@nasa.gov
301-286-4638

Authorizing NASA Official: Jerome Bennett
Web Curator: Lara Clemence (GST)
Web Design: Judy Laue

Last Modified: August 15, 2003

NASA logo

EOE

VISITING STUDENT ENRICHMENT PROGRAM

Quantum Mechanical Simulations on a Beowulf Cluster