|
At one of my interviews for a position with Lockheed
Martin Co., I was asked what the difference was between a
geostationary and a geosynchronous orbit.
Unfortunately, at the time I was quite confused, because I
had never heard of a geostationary orbit, though it
sounded much like what I thought was a geosynchronous
orbit. As it turns out, a geostationary orbit is a member
of the set or family of geosynchronous orbits, but it
is a special case of a geosynchronous orbit which
is circular and lies in the Earth's equatorial
plane. Let us first look at what constitutes a
geosynchronous orbit.
For me, one of the more interesting results of orbital
mechanics is that there is a unique radius of a
circular orbit
which will produce an orbital period equal to the
rotational period of the earth (approximately 24
hours). Such an orbit is called a geosynchronous
orbit, and its radius is 42,300 km from the center of
the Earth (about 35,900 km from the surface of the
Earth). We can calculate this by equating the
gravitational force on the orbiting satellite to the
centripetal force. That is, in order to maintain its
orbit, the gravitational force must be equal to the
centripetal force required to keep the satellite in
uniform circular motion.
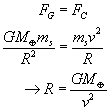
Now we need an expression for the linear velocity of the
orbit. We know that the time it takes the satellite
to complete one orbit is the total length of
the orbit divided by the linear velocity
(distance/velocity = time).
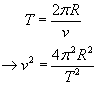
So our final expression for the radius of orbit is
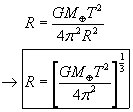
A satellite in a circular geosynchronous orbit will
oscillate in a vertical line with a period
approximately equal to 24 hours. The angular amplitude of the
oscillation is equal to the angle between the orbital
plane of the satellite and the equatorial plane of the
Earth. Thus, if the angle between the orbital plane
and the equatorial plane is zero, the amplitude of
oscillation will be zero, and the satellite will
remain in a single location on the sky. This is why
the geosynchronous orbit in the equatorial plane is
called a geostationary orbit. Pictured below is a
schematic image of a geosynchronous orbit and a
geostationary orbit around the Earth.

I should also mention that communication satellites
often follow elliptical geosynchronous orbits,
which trace out an analemma (a figure eight) on the
sky. The shape of the analemma is determined by the
shape of the elliptical orbit.
|