abstract.

In this lab we recorded a sample phrase with a 400 Hz noise behind it. We converted all the sample recordings into the frequency domain in order to make them easier to work with. We then used three different methods to try and filter out the noise, a subtraction method, a frequency threshold method and a frequency suppression method. Each of these methods worked pretty well but the frequency threshold method worked the best because it almost completely eliminated the noise without messing up the sample phrase.

introduction and problem definition.

The task in this experiment was to eliminate the noise in a corrupt voice sample using different techniques. The overall approach to doing this was to first convert noise and corrupt samples into the frequency domain using the Fourier Transform. This converted the sample values into complex numbers which we then converted into magnitudes and phases. This conversion of the samples into the frequency domain makes the elimination of the noise much easier to perform because it eliminates the integration necessary to perform convolution in the time domain.
      We then used three different methods in order to eliminate the noise. After performing these methods, we then converted the cleaned up signal back into the time domain using the inverse Fourier Transform with the new cleaned up magnitudes and the old phases of the sample. This then allowed us to hear the cleaned up signal and to see if in fact the noise had been eliminated.

methods and experiments.

In this experiment we used three different methods to eliminate the 400 Hz noise from our sample recording. Before performing the noise elimination we converted all the sample recordings into the frequency domain using the discrete Fourier Transform (DFT). This makes the samples easier to work with because while the convolution in the time domain involves integration and calculus, it only involves simple algebra in the frequency domain. This makes the elimination of a sample noise much easier to do in the frequency domain than it is in the time domain. We then took the absolute value of the values in the frequency domain in order to find the magnitude of the complex number that resulted when we preformed the DFT.
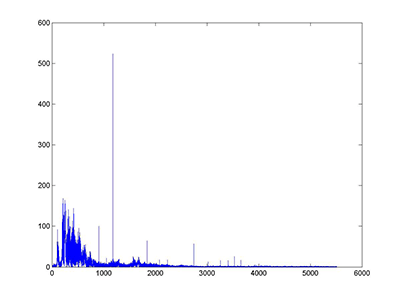
The first method we used to eliminate the noise was the subtraction method. For the subtraction method we subtracted the magnitude of the noise signal in the frequency domain from the magnitude of corrupt signal in the frequency domain. We then converted the cleaned up signal back into the time domain by taking the inverse Fourier Transform for the new magnitude and the old phase. This method worked pretty well but did not completely eliminate the noise.
      We then tried a threshold magnitude method where we picked a threshold magnitude of the noise signal and then reduced the magnitude of the corrupt signal for any frequency that went above this threshold. Our threshold magnitude for the noise signal was 10. Any frequency value that had a value in the noise sample above 10 had its corresponding magnitude in the corrupt sample multiplied by .001. We then again used the inverse Fourier Transform and the old phase to convert the signal back into the time domain. This method worked very well because it almost completely eliminated the noise without changing the sample phrase. However, this is only because our noise sample and the noise in our corrupt sample matched up almost perfectly. I this had not been the case and the samples were slightly off from each other, this method could have missed the noise in the corrupt sample and done a poor job eliminating the noise. If this had been the case we would have had to blur the noise signal in order to make sure that all the noise in the corrupt sample was eliminated even if it did not match up perfectly with the noise sample.
      For the third method we targeted specific frequencies and tried to suppress them. We could use this method because we knew the frequency at which the noise was occurring. Therefore, we could easily suppress that frequency and its harmonics. We then again converted this signal back into the time domain using Fourier Transform and the old phase. However, this method did not work very well because it still allowed through a lot of the noise.
We also preformed two extinctions. For extinction 3, we created a corrupt sample where you could hardly hear the speaker and then we preformed the subtraction method of noise elimination on it. This method, however, also eliminated much of the voice sample as well. We preformed extinction 5 where we filtered out the phrase but not the noise. We did this by using method three, the suppression of specific frequencies, and just changing it to suppress everything except the 400 Hz and its harmonics. This worked very well and eliminated the entire phrase while still letting through the noise.

results.

:: zipped files:
these files should be downloaded to the Matlab user directory to run the M-files

:: Sound Files

noise
corrupt
clean phrase

:: M-files

method1
method2
method3

:: Figures

noise

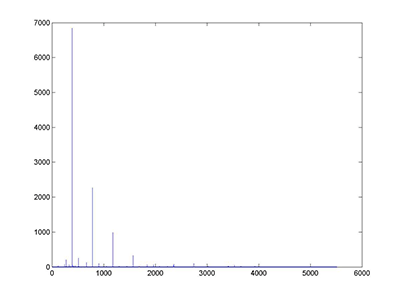
noise - time domain

corrupt speech

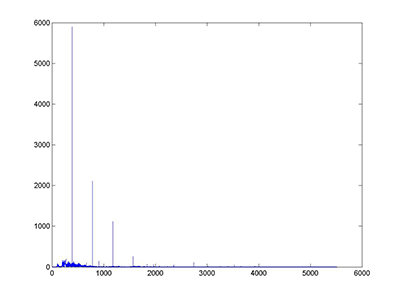
corrupt speech - time domain

clean phrase - time domain

method 1 - clean

method 2 - clean

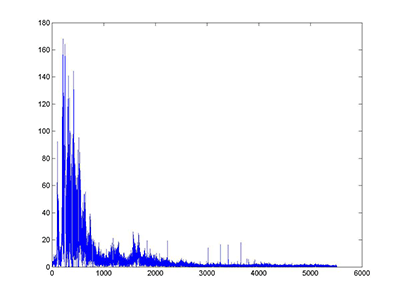
method 2 - clean - time domain

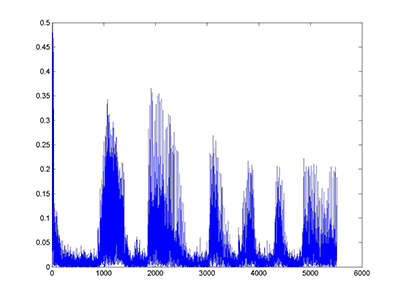
method 3 - clean

discussion.

Which method of noise reduction worked best for this task?
The 2nd method worked best. The 1st and the 3rd methods worked well, but they weren’t as efficient as the first one. Additionally, the 1st method was slightly better than the third.

The spectrum of the recorded noise is not just 400Hz and its harmonics. Why are there other frequencies in the signal?
There was other background noise (i.e. other malicious groups working in the background)

Did the last method based on suppression of a known frequency work better or worse than one based on a model of the actual noise? Why, why not?
It worked worse because it didn’t take care of the background noise. It would have worked much better if the noise signal didn’t include anything other than the 400Hz frequency and its harmonics.

Why is it a good idea to blur the noise spectrum prior to using it for suppression?
It’s a good idea to blur the signals because if the noise in the corrupt signal doesn’t exactly match the noise signal, then the method will fail to reduce the correct frequency and most of the noise will remain in the corrupt signal. However, blurring will spread out the noise signal and so more frequencies near the noise frequency will be reduced in the corrupt signal resulting in a much better chance of eliminating the noise. This could potentially reduce some of the voice signal but it usually significantly reduces the noise signal while having negligible effect on the voice signal.

Why do we try to keep the phase the same as the original signal when executing subtraction in the Fourier domain? What happens if you just set the phase to an arbitrary value (you might try this for real)?
The phase contains the time data; therefore, using the original phase would give us the right sounds at the right time whereas setting the phase to an arbitrary value would yield a signal with sounds at relatively random times. For instance, “engineering at Swarthmore” might sound like “egnriga Satmrniern twrhoe” (which of course makes no sense).

How could you use the concepts presented in this lab to build a real-time noise cancellation device for a cockpit in a jet or helicopter?
We could have two microphones, one for recording the pilot’s [corrupt] voice and one recording the ambient noise (placed away from the pilot so that the pilot’s voice will not be recorded). Continuously applying the Fourier transform to each of the signals and performing one of the three methods would act as a noise cancellation device. Therefore the pilot’s voice, cleaned of the excess noise, could be transmitted through the device reducing the possibility of fatal accidents caused by the miscommunication between pilots and control towers.

extensions.

3. Try creating a corrupt sample where you can hardly hear the speaker and see if one of the subtraction methods will still work.
With the sample where one can hardly hear the speaker, the subtraction method no longer works because, even if the noise is reduced, it’s not completely taken care of. Also, there is background noise in the noise sample, which when subtracted from the voice sample eliminates much of the voice signal. This is because the voice is not much louder than the background noise. Therefore, the result is a signal with reduced noise but not a pure voice signal; in fact, the voice can barely be heard.

5. Try filtering out your voice and leaving just the 400Hz noise (why not?)
Using the inverse-3rd method, where everything but the 400Hz frequency and its harmonics are eliminated, we can get a signal very similar to the pure noise signal. This wouldn’t work with the 1st method, because we wouldn’t have the clean voice signal to subtract from the corrupt signal.